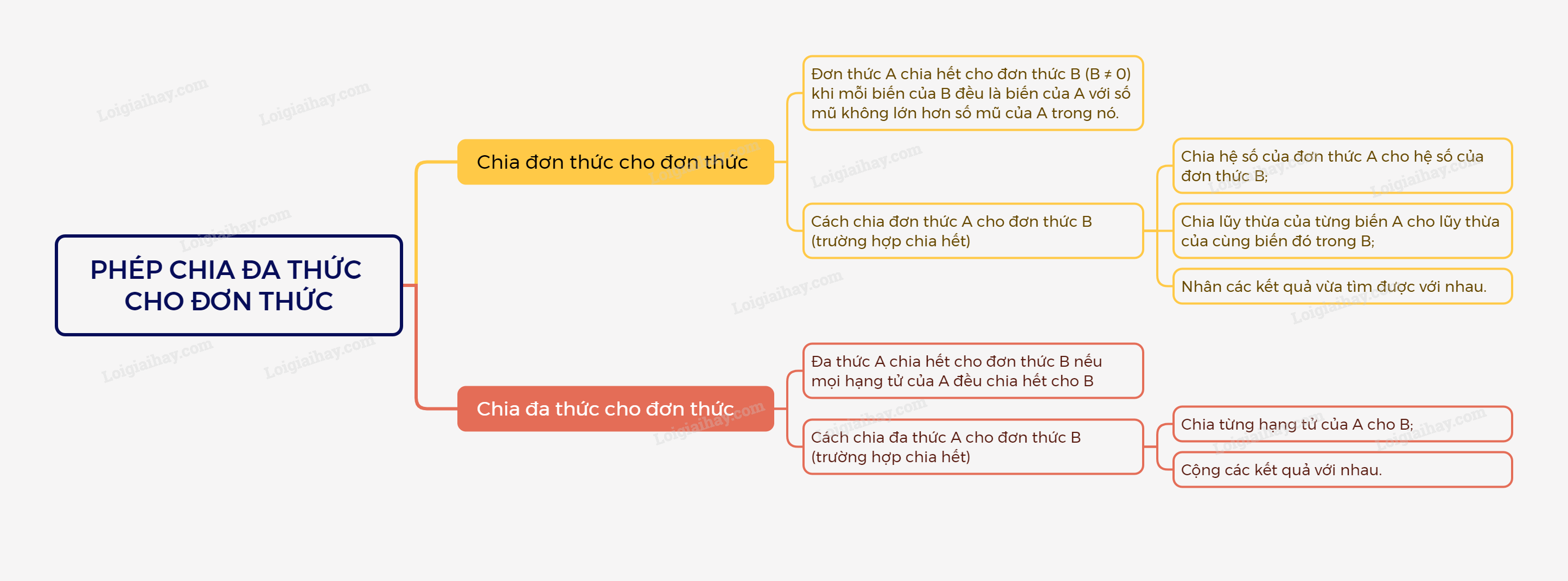
Chia đơn thức cho đơn thức như thế nào?

a. Đơn thức A chia hết cho đơn thức B(B≠0)

khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.

b. Muốn chia đơn thức A cho đơn thức B (trường hợp chia hết), ta làm như sau:

– Chia hệ số của đơn thức A cho hệ số của đơn thức B;

– Chia lũy thừa của từng biến A cho lũy thừa của cùng biến đó trong B;

– Nhân các kết quả vừa tìm được với nhau.

Ví dụ:

\[ 16x^4y^3: -8x^3y^2\] 

\[ (16:(-8)).(x^4:x^3).(y^3:y^2)\] 

\[ =(-2).(x).(y)\] 

\[ =-2xy\] 

+ Chia đa thức cho đơn thức như thế nào?

Đa thức A chia hết cho đơn thức B nếu mọi hạng tử của A đều chia hết cho B.

Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.

Ví dụ:

\[ (x^2y+y^2x): xy\] 

\[ (x^2y:xy)+(y^2x:xy)\] 

\[ =(x)+(y)\] 

\[ =x+y\] 

\[ (-12x^4y+4x^3-8x^2y^2): -4x^2\] 

\[ (-12x^4y:-4x^2)+(4x^3:-4x^2)+(-8x^2y^2:-4x^2)\] 

\[ =(3x^2y)+(-x)+(2y^2)\] 

\[ =3x^2y-x+2y^2\] 

Cộng (hay trừ) hai đa thức tức là thu gọn đa thức nhận được sau khi nối hai đa thức đã cho bởi dấu “+” (hay dấu “–”)

Phép cộng đa thức cũng có các tính chất giao hoán và kết hợp tương tự như phép cộng các số.

+ Giao hoán: A + B = B + A

+ Kết hợp: (A + B) + C = A + (B + C)

Ví dụ:

cho 2 đa thức

\[ A= x^2-2y+xy+1\]

\[ B= x^2+y-x^2y^2-1\]

Tìm đa thức C = A +B

C=A+B

\[ C = (x^2-2y+xy+1)+(x^2+y-x^2y^2-1)\]

\[ C = x^2-2y+xy+1)+(x^2+y-x^2y^2-1\]

\[ C = (x^2+x^2)+(-2y+y)+xy-x^2y^2+(1-1)\]

\[ C = 2x^2-y+xy-x^2y^2\]

Vậy đa thức  C =

\[ 2x^2-y+xy-x^2y^2\]

Đa thức là một tổng của những đơn thức.

Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).

Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.

Ví dụ:

\[ x^2-4x+3;x^2+3xyz^2-yz+1;(x+3y)+(2x-y) \] là đa thức

\[ \frac{(x+3y)}{(2x-y)};\frac{(x^2+2)}{(x^2-y^2)} \] không phải là đa thức

\[ x^2-4x+3   \] có 3 hạng tử

\[ x^2;-4x;3   \]

\[ x^2+3xyz^2-yz+1   \] có 3 hạng tử

\[ x^2;3xyz^2;-yz;1 \]

Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.

Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.

Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

Đa thức thu gọn

là đa thức không chứa hai hạng tử nào đồng dạng.

Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.

Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

Ví dụ:

\[ A=x^3-2x^2y-x^2y+3xy^2+y^2 \]

\[=x^3-3x^2y+3xy^2+y^2 \]

Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Một số khác 0 tùy ý được coi là một đa thức bậc 0.

Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.