Category Archives: Toán lớp 8
1. Số tự nhiên có từ bao giờ ?
Những khái niệm đầu tiên về số tự nhiên đã có từ thời cổ xưa. Những khái niệm đó phát sinh từ việc đếm các đồ vật, con người, vật nuôi, hoa quả … Kết quả của phép đếm là các số một, hai, ba, …. Các số đó ngày nay gọi là số tự nhiên.
2. Số tự nhiên là những số nào?
Các số: 0 , 1 , 2 , 3, … , 9 , 10 ,…., 99 , 100 ,…, 999 , 1 000 , …. là các số tự nhiên
3. Thế nào là dãy số tự nhiên?
Các số tự nhiên sắp xếp theo thứ tự từ bé đến lớn tạo thành dãy số tự nhiên: 0 , 1 , 2 , 3 , 4 , 5 , 6 , …
Để có hình ảnh về dãy số tự nhiên, ta có thể biểu diễn các số tự nhiên trên tia số:
Số 0 ứng với điểm gốc của tia số. Mỗi số tự nhiên ứng với một điểm trên tia số.
4. Dãy số tự nhiên có đặc điểm gì?
Trong dãy số tự nhiên:
– Thêm 1 vào bất kì số nào cũng được số tự nhiên liền sau số đó. Vì vậy, không có số tự nhiên lớn nhất và dãy số tự nhiên có thể kéo dài mãi.
– Chẳng hạn: Số 1 000 000 thêm 1 được số tự nhiên liền sau là 1 000 001, số 1 000 001 thêm 1 được số tự nhiên liền sau là 1 000 002, …
– Bớt 1 ở bất kì số nào (khác số 0) cũng được số tự nhiên liền trước số đó. Không có số tự nhiên nào liền trước số 0 nên 0 là số tự nhiên bé nhất. Hai số tự nhiên liên tiếp thì hơn hoặc kém nhau 1 đơn v
Khái niệm phân số:
Phân số bao gồm có tử số và mẫu số, trong đó tử số là một số tự nhiên viết trên dấu gạch ngang, mẫu số là số tự nhiên khác 0
viết dưới dấu gạch ngang.
Cách đọc phân số: khi đọc phân số ta đọc tử số trước rồi đọc “phần”, sau đó đọc đến mẫu số.
\[\frac{2}{3};\frac{5}{10};\frac{3}{4}\]
là các phân số
Chú ý:
1) Có thể dùng phân số để ghi kết quả của phép chia một số tự nhiên cho một số tự nhiên khác 0
. Phân số đó cũng được gọi là thương của phép chia đã cho.
Ví dụ:
\[1:3=\frac{1}{3};2:5=\frac{2}{5}\]
2) Mọi số tự nhiên đều có thể viết thành phân số có mẫu số là 1.
Ví dụ:
\[3=\frac{3}{1};5=\frac{5}{1}\]
3) Số 1 có thể viết thành phân số có tử số và mẫu số bằng nhau và khác 0.
\[1=\frac{9}{9};1=\frac{8}{8}\]
4) Số 0 có thể viết thành phân số có tử số là 0 và mẫu số khác 0.
\[0=\frac{0}{9};0=\frac{0}{8}\]
Do đó, tỉ lệ chiều cao giữa cột màu xanh và cột màu vàng không bằng tỉ lệ hai số mà chúng biểu diễn vì trong Biểu đồ a) người ta chia các giá trị từ 950 đến 990 (còn phần giá trị từ 0 đến 950 đã bị rút ngắn).
Thống kê món ăn được ưa thích
| Món ăn | Phở | Nem | Bánh mì |
| Số lượt bình chọn | 972 | 987 | 955 |
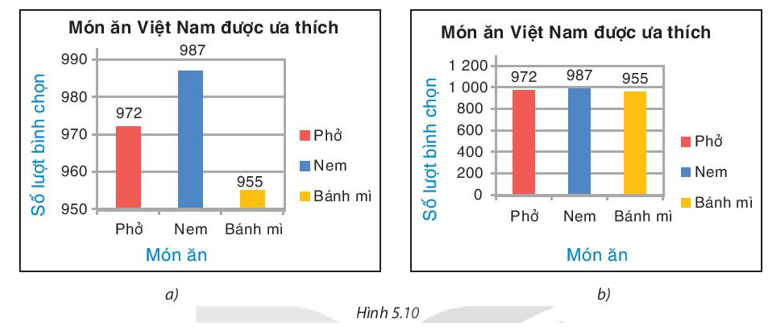
Trong Biểu đồ a), cột màu xanh chiếm hơn 3,5 ô; cột màu vàng chiếm khoảng 1,5 ô.
Khi đó, tỉ lệ chiều cao giữa cột màu xanh và cột màu vàng trong Biểu đồ a) khoảng:
\[\frac{3,5}{1,5}=\frac{7}{3} \approx2,03\]
Tỉ lệ số lượt bình chọn nem và bánh mì là:
\[\frac{987}{955} \approx1,03\]
2. Đọc và phân tích số liệu từ biểu đồ
Chú ý: Khi phân tích số liệu, ta có thể kết hợp thông tin từ hai hay nhiều biểu đồ.
Để so sánh sự thay đổi theo thời gian của hai hay nhiều đại lượng, người ta thường biểu diễn chúng trên cùng biểu đồ.
Các biểu đồ sau cho biết cơ cấu năng lượng được khai thác, sản xuất trong nước các năm 2018 và 2019.

Các dạng năng lượng
Các loại năng lượng
Than
Dầu thô
Khí thiên nhiên
Nhiên liệu sinh học
Tỷ lệ (%)
48,23
20,59
16,78
14,62
| Các loại năng lượng | Than | Dầu thô | Khí thiên nhiên | Nhiên liệu sinh học |
| Tỷ lệ (%) | 48,23 | 20,59 | 16,78 | 14,62 |
Sự thay đổi cơ cấu năng lượng được khai thác, sản xuất trong các nước năm 2019 so với năm 2018.
– Than giảm khoảng 0,03% (từ 48,37% xuống còn 45,02%);
– Dầu thô tăng khoảng 2,6% (từ 20,59% lên đến 23,19%);
– Khí thiên nhiên tăng khoảng 0,31% (từ 16,78% lên đến 17,09%);
– Nhiên liệu sinh học tăng khoảng 0,08% (từ 14,62% lên đến 14,70%).

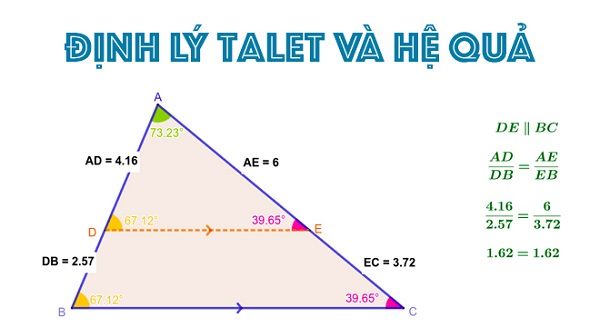
Tính chất của đường phân giác
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
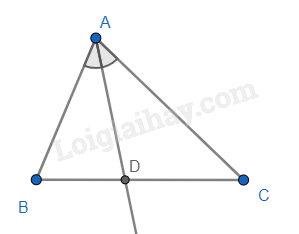
Chú ý: Trong tam giác ABC, nếu D là điểm thuộc đoạn thẳng BC và thỏa mãn
\[\frac{DB}{DC}=\frac{AB}{AC}\]
thì AD là đường phân giác của góc A
Ví dụ:


Hình bình hành
1. Định nghĩa:
là tứ giác có các cạnh đối song song.

Tứ giác ABCD là hình bình hành
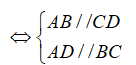
2. Tính chất

Trong hình bình hành:
• Các cạnh đối bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
ABCD là hình bình hành, AC cắt BD tại O. Khi đó:
• AB = CD, AD = BC
3.Dấu hiệu nhận biết
• Tứ giác có các cạnh đối song song là hình bình hành.
• Tứ giác có các cạnh đối bằng nhau là hình bình hành.
• Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
• Tứ giác có các góc đối bằng nhau là hình bình hành.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
4. Diện tích hình bình hành

Diện tích của hình bình hành bằng chiều cao nhân với cạnh đáy tương ứng của nó.
S = a.h
h: chiều cao của hình bình hành
a: độ dài cạnh đáy tương ứng
Cho hình bình hành ABCD, kẻ 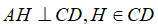
S = AH.CD
5. Chu vi hình bình hành
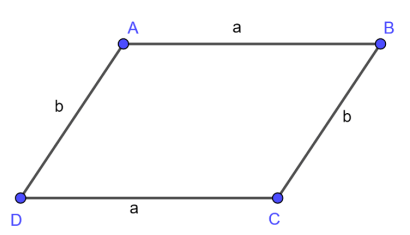
Chu vi của hình bình hành bằng tổng độ dài bốn cạnh của hình bình hành ( nói cách khác, chu vi hình bình hành bằng hai lần tổng độ dài một cặp cạnh kề nhau bất kì của hình bình hành.
P = a + a + b + b = 2(a + b)
Hình thoi
1. Khái niệm
Hình thoi là tứ giác có bốn cạnh bằng nhau.
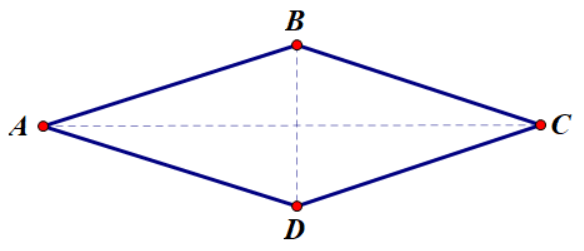
2. Tính chất
Trong hình thoi:
a. Hai đường chéo vuông góc với nhau;
b. Hai đường chéo là các đường phân giác của các góc trong hình thoi.
3. Dấu hiệu nhận biết hình thoi
a. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
b. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
c. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Hình vuông
1. Khái niệm
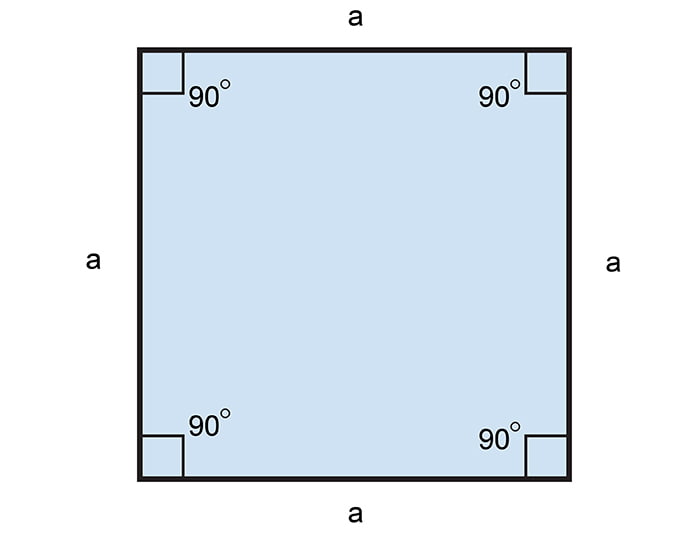
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
2. Tính chẩt
Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường và là các đường phân giác của các góc của hình vuông.
3. Dấu hiệu nhận biết hình vuông
a. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
b. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

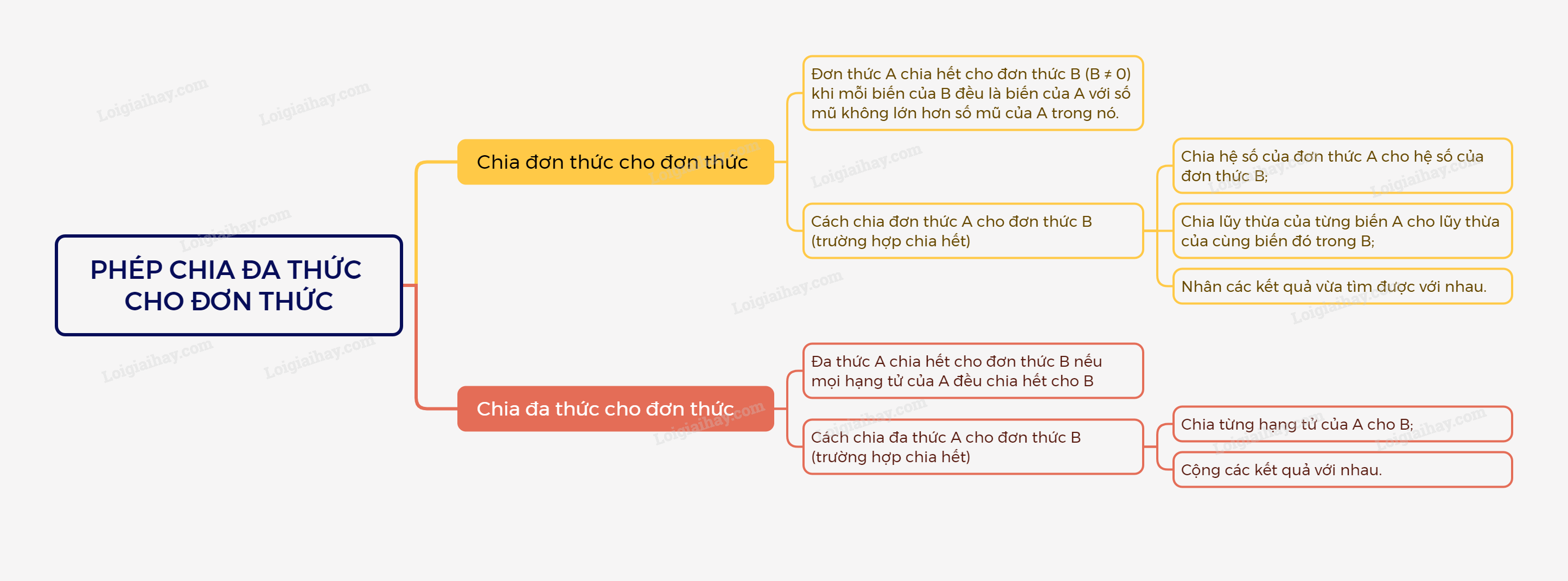
Chia đơn thức cho đơn thức như thế nào?
a. Đơn thức A chia hết cho đơn thức B(B≠0)
khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
b. Muốn chia đơn thức A cho đơn thức B (trường hợp chia hết), ta làm như sau:
– Chia hệ số của đơn thức A cho hệ số của đơn thức B;
– Chia lũy thừa của từng biến A cho lũy thừa của cùng biến đó trong B;
– Nhân các kết quả vừa tìm được với nhau.
Ví dụ:
\[ 16x^4y^3: -8x^3y^2\]
\[ (16:(-8)).(x^4:x^3).(y^3:y^2)\]
\[ =(-2).(x).(y)\]
\[ =-2xy\]
+ Chia đa thức cho đơn thức như thế nào?
Đa thức A chia hết cho đơn thức B nếu mọi hạng tử của A đều chia hết cho B.
Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.
Ví dụ:
\[ (x^2y+y^2x): xy\]
\[ (x^2y:xy)+(y^2x:xy)\]
\[ =(x)+(y)\]
\[ =x+y\]
\[ (-12x^4y+4x^3-8x^2y^2): -4x^2\]
\[ (-12x^4y:-4x^2)+(4x^3:-4x^2)+(-8x^2y^2:-4x^2)\]
\[ =(3x^2y)+(-x)+(2y^2)\]
\[ =3x^2y-x+2y^2\]

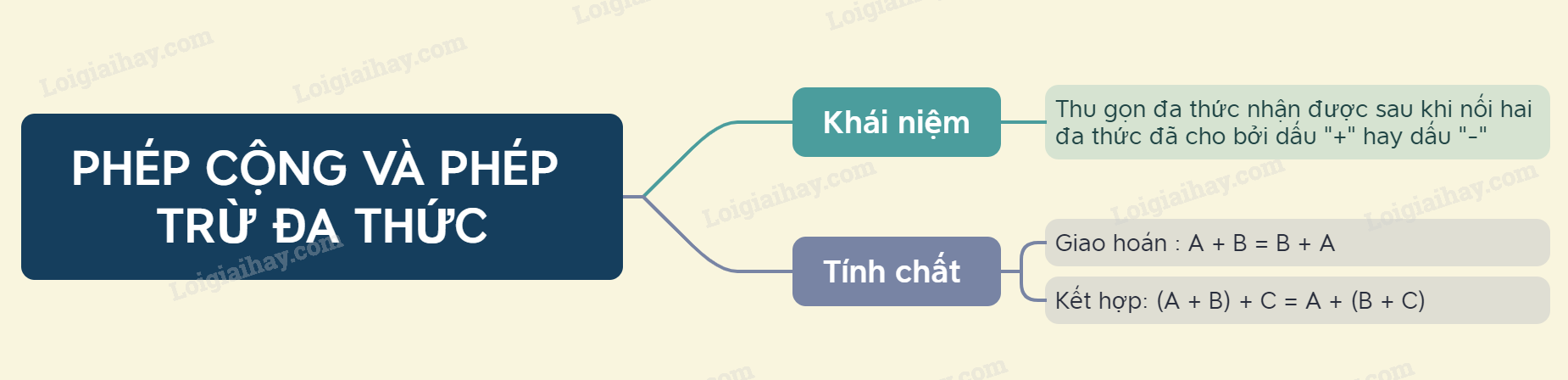
Cộng (hay trừ) hai đa thức tức là thu gọn đa thức nhận được sau khi nối hai đa thức đã cho bởi dấu “+” (hay dấu “–”)
Phép cộng đa thức cũng có các tính chất giao hoán và kết hợp tương tự như phép cộng các số.
+ Giao hoán: A + B = B + A
+ Kết hợp: (A + B) + C = A + (B + C)
Ví dụ:
cho 2 đa thức
\[ A= x^2-2y+xy+1\]
\[ B= x^2+y-x^2y^2-1\]
Tìm đa thức C = A +B
C=A+B
\[ C = (x^2-2y+xy+1)+(x^2+y-x^2y^2-1)\]
\[ C = x^2-2y+xy+1)+(x^2+y-x^2y^2-1\]
\[ C = (x^2+x^2)+(-2y+y)+xy-x^2y^2+(1-1)\]
\[ C = 2x^2-y+xy-x^2y^2\]
Vậy đa thức C =
\[ 2x^2-y+xy-x^2y^2\]

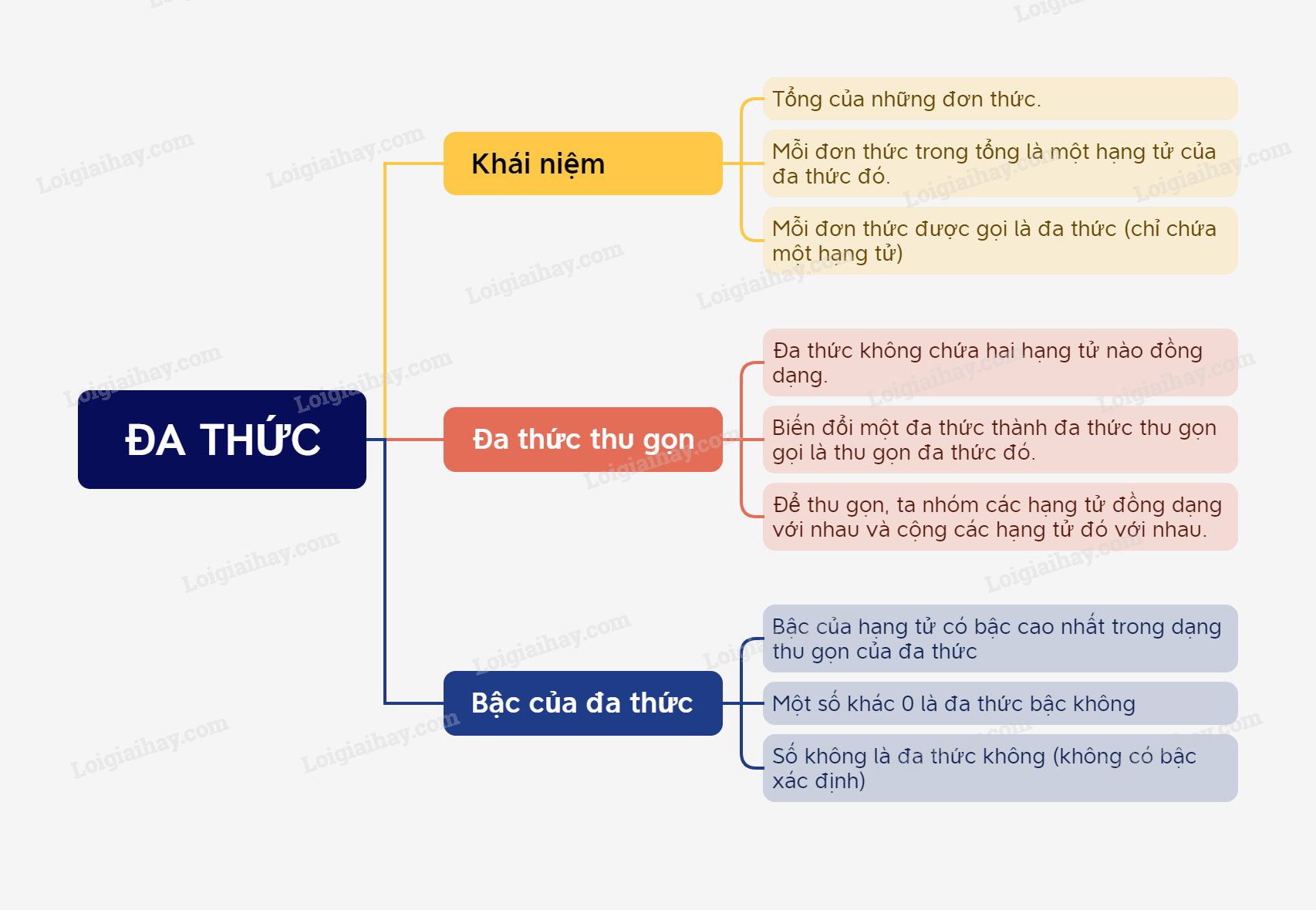
Đa thức là một tổng của những đơn thức.
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ:
\[ x^2-4x+3;x^2+3xyz^2-yz+1;(x+3y)+(2x-y) \] là đa thức
\[ \frac{(x+3y)}{(2x-y)};\frac{(x^2+2)}{(x^2-y^2)} \] không phải là đa thức
\[ x^2-4x+3 \] có 3 hạng tử
\[ x^2;-4x;3 \]
\[ x^2+3xyz^2-yz+1 \] có 3 hạng tử
\[ x^2;3xyz^2;-yz;1 \]
Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Đa thức thu gọn
là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Ví dụ:
\[ A=x^3-2x^2y-x^2y+3xy^2+y^2 \]
\[=x^3-3x^2y+3xy^2+y^2 \]
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Một số khác 0 tùy ý được coi là một đa thức bậc 0.
Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.